伊利诺伊大学的研究人员Kyle Smith、博士生dr . Habibur Rahman和Vu Do、硕士生Colby Warden和刚毕业的研究生Irwin Loud IV (MSME 2023)在《流体物理学》上发表了他们的新流道设计理论(正在申请专利)。

　　他们的论文《低雷诺数下均匀流动的紧凑低压歧管》也被该杂志的编辑选为专题文章。

　　“我认为，从机械工程的角度来看，真正酷的事情是，在我们引入的这种设计范式中，我们利用了歧管内的压力梯度，使流动均匀，”机械科学与工程副教授史密斯说。

　　通常根据其用途(例如，进气或排气)进行分类，歧管作为中空体，空气或水等流体通过它从一个空间过渡到另一个空间。例如，汽车的进气歧管有助于空气进入发动机的气缸。

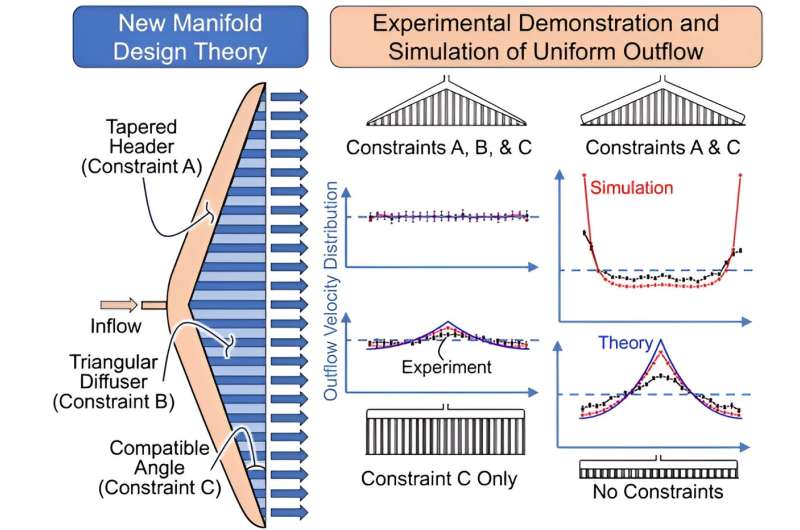
　　该小组的理论提出了一种完全不同于文献中长期存在的流形设计理论的设计策略，后者优先考虑在流形内实现均匀的压力。他们的理论阐明了必须满足的三个设计约束，其中第一个是战略性地减小歧管总管或进气的横截面。

　　“根据你使用的横截面类型，头部通道的形状，锥形函数采用不同的形式，”史密斯在应用该理论时说。“这些都是基于物理的限制，工程师可以将其应用到歧管的设计中。”

　　第二个约束规定扩散器区域，或出口，应该有均匀间隔的通道排列成三角形结构。第三个约束说明了应该应用于该区域的角度。

　　“最终，我们选择了锥形导流管、三角形导流管歧管，因为从理论上讲，这是唯一一种能够在所有出口通道产生均匀流速的导流管，”Loud说，并回忆起他们还研究过其他配置，如直管、三角形导流管和直管、矩形导流管。

　　这篇论文描述了研究人员的实验过程，为此Loud最初3d打印了歧管原型。该小组将随后的迭代加工出透明的丙烯酸，然后从基于染料的流动可视化中收集数据，分析染色流体流经歧管进入未染色溶液的图像。

　　拉赫曼谈到他所做的实验时说:“一个主要的挑战是气泡的捕获。我们最终通过使用表面活性剂克服了这个障碍。作为一名新的实验学家，做这些实验对我来说是一种挑战和激励。”他们的实验结果与他们的理论和计算机模拟结果非常吻合。

　　Smith说:“我们的论文讨论了满足所有三个约束的流形与包含某些约束但忽略其他约束的流形的比较。”“我们证明，同时满足这三个约束条件，可以在最宽的流量范围内产生最均匀的流动和均匀的流动。”

　　他们的文章重点介绍了一种单一歧管的设计，该歧管可以将流体从一个输入分配到多个出口，这是实现出口流动均匀性的最具挑战性的歧管配置。然而，该理论可以广泛应用，包括两个歧管系统，以实现多流的进排气均匀流动。

　　史密斯的研究小组在海水淡化实验中观察到的现象激发了他对一种新的设计理论的追求，在这种现象中，含盐溶液通过一个歧管流过电极。

　　“我们最初致力于设计一个更大版本的类似电池的海水淡化液流电池，”Loud回忆起一年多前与Smith和同学Do在实验室的工作。“其中一个主要考虑因素是确保电解液均匀分布到电极的前缘。”

　　Do指出，在放大设计中，由于前缘的尺寸将增加一倍，研究小组需要重新考虑歧管如何将流体输送到电极。“我不确定我们中是否有人预见到设计过程会如此广泛，”Loud谈到最终的研究结果时说。

　　这个项目对史密斯个人也有重要意义。“我的父亲，里克·史密斯，是一个没有大学学位的发明家，他为赛车设计进气歧管和其他发动机部件，”史密斯说。

　　“当我还是个孩子的时候，我和他一起参加了比赛和他的制造车间。我最早的记忆之一是我爸爸在我的苏斯博士的书上画发明草图。当我意识到我们有机会做一些对歧管设计有广泛影响的事情时，我非常兴奋，因为我们可以在我长期接触的领域做一些创新的事情。”

　　锥形头、三角形扩散管歧管可以实现均匀流动，占地面积不到同类分岔歧管的四分之一。对于必须将加压流体分布在电极上的电化学装置，如液流电池、燃料电池、电解槽和电化学脱盐电池，均匀分布应导致均匀反应，换句话说，提高效率。Smith打算继续以该理论为基础，提高流体管理效率。

　　此外，该小组的理论可以适用于农业和医疗领域等广泛的各种应用。此外，他们的理论也可应用于其他流态和其他类型的流体。

　　史密斯说:“我们有机会利用这一理论的基本抽象原则，并在许多其他情况下以此为基础。”

　　更多信息:Kyle C. Smith等人，一种紧凑的低雷诺数均匀流动的低压歧管，流体物理(2024)。DOI: 10.1063/5.0211073期刊信息:流体物理学由伊利诺伊大学格兰杰工程学院提供引用:研究人员首次推出新颖的流形设计理论(2024年，6月5日)从https://techxplore.com/news/2024-06-debut-manifold-theory.html检索2024年6月5日此文档受版权保护。除为私人学习或研究目的而进行的任何公平交易外，未经书面许可，不得转载任何部分。内容仅供参考之用。